UNIWERSUM ROZWOJU, 2025
Matematyczne Sztuczki i Triki
Zaskocz Znajomych (i Egzaminatorów!) Liczbami!
Co to układy równań?
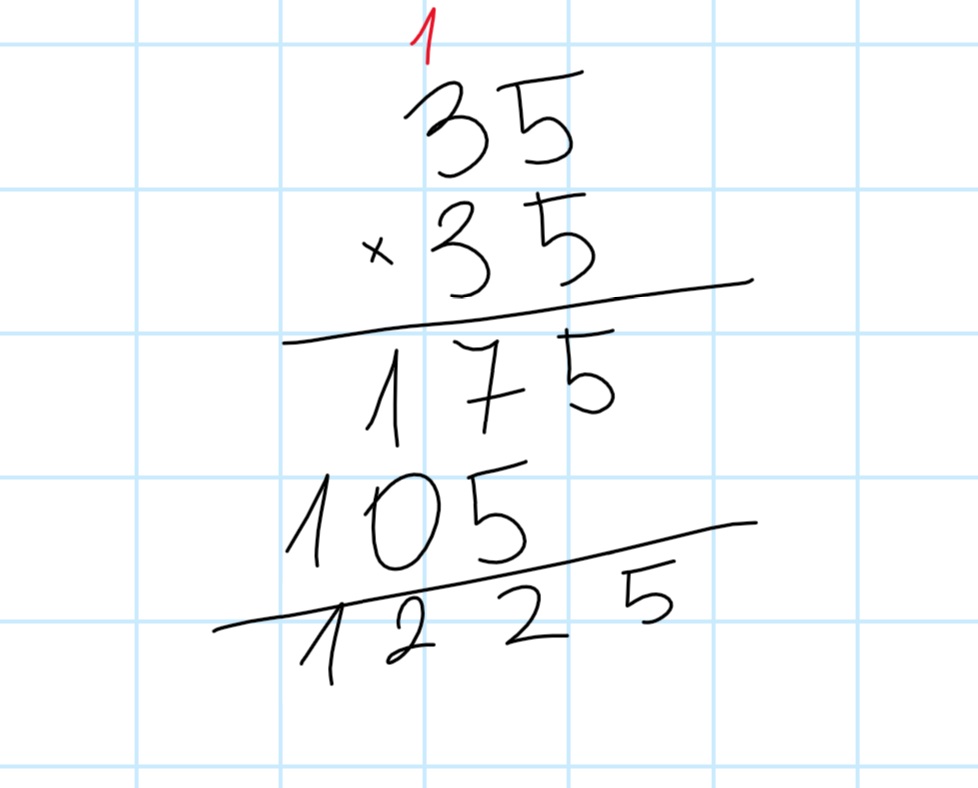
Matematyczne Sztuczki i Triki:
Zaskocz Znajomych (i Egzaminatorów!) Liczbami!
Przed Wami ważne wyzwanie – egzamin z matematyki. Wiemy, że czasami liczby i wzory mogą wydawać się skomplikowane, ale dzisiaj pokażemy Wam, że matematyka może być też fascynująca i pełna niespodzianek! Przygotowaliśmy dla Was kilka sprytnych sztuczek i trików, które nie tylko zadziwią Waszych znajomych, ale także mogą okazać się pomocne na egzaminie, usprawniając niektóre obliczenia i dając Wam pewność siebie. Gotowi na dawkę matematycznej magii? Zaczynamy!
jak tego dokonać ?
Szybkie Kwadraty Liczb Kończących się na 5
Ta sztuczka pozwoli Wam błyskawicznie podnieść do kwadratu każdą liczbę naturalną, która kończy się cyfrą 5.
Jak to działa?
Weźmy liczbę, na przykład 35.
- Odrzuć ostatnią cyfrę, czyli 5. Zostaje nam 3.
- Pomnóż tę liczbę przez liczbę od niej o jeden większą: 3×(3+1)=3×4=12.
- Do wyniku dopisz na końcu 25.
Zatem, 35 do kwadratu to 1225. Sprawdźcie na kalkulatorze – działa!
Przykłady:
- $15^2 = (1 \times (1+1))25 = 225$
- $25^2 = (2 \times (2+1))25 = 625$
- $35^2 = (3 \times (3+1))25 = 1225$
- $45^2 = (4 \times (4+1))25 = 2025$
- $55^2 = (5 \times (5+1))25 = 3025$
- $65^2 = (6 \times (6+1))25 = 4225$
- $75^2 = (7 \times (7+1))25 = 5625$
- $85^2 = (8 \times (8+1))25 = 7225$
- $95^2 = (9 \times (9+1))25 = 9025$

Dlaczego to działa ?
Każdą liczbę kończącą się na 5 możemy zapisać jako 10n+5. Podnosząc ją do kwadratu, otrzymujemy:
\( (10n + 5)^2 = (10n)^2 + 2 \cdot 10n \cdot 5 + 5^2 = 100n^2 + 100n + 25 = 100n(n+1) + 25 \)
Widzimy więc, że wynik składa się z liczby \(n(n+1)\) pomnożonej przez 100 (czyli dopisujemy dwa zera), a następnie dodajemy 25.
metoda przeciwnych współczynników
układ równań 1.
zadanie zaczerpnięte ze zbioru zadań MATEMATYKA 1, s.156, z. 5.16 b)
układ równań 2.
zadanie zaczerpnięte ze zbioru zadań MATEMATYKA 1, s.157, z. 5.17 a)
układ równań 3.
zadanie zaczerpnięte ze zbioru zadań MATEMATYKA 1, s.158, z. 5.21 a)
układ równań 4.
zadanie zaczerpnięte ze zbioru zadań MATEMATYKA 1, s.163, z. 5.38 d)
układ równań 5.
zadanie zaczerpnięte ze zbioru zadań MATEMATYKA 1, s.164, z. 5.45 d)
metoda przeciwnych współczynników
układ równań 1.
układ równań 2.
układ równań 3.
układ równań 4.
układ równań 5.
Enhanced Brain Connectivity in Children with Music Training
Music training enhances the neural networks involved in executive function and transfer of learning
Linking music to spatial reasoning: effects of musical experience on spatial performance
The effects of music instruction on mathematics achievement

